Usage Examples for MDDC in R • MDDC

Introduction

This vignette contains various examples that illustrate usage of MDDC.

Installation

The MDDC package is available on CRAN and can be installed using the following code. Additionally, the development version can be found on GitHub.

install.packages("MDDC")

We load the MDDC package using the following line:

library(MDDC)

Dataset

We have included an adverse event dataset curated from FDA Adverse Event Reporting System (FAERS) called statin49 dataset which we will be using for describing the functionalities of MDDC. statin49 was downloaded and processed from the FAERS database, covering the period from the third quarter of 2014 (Q3 2014) to the fourth quarter of 2020 (Q4 2020). This dataset is a $50\times 7$ contingency table. The first 49 rows represent 49 important adverse events (AEs) associated with the statin class, while the final row aggregates the remaining 5,990 AEs.

The dataset statin49_AE_idx lists the cluster index of each AE in the statin49 dataset. The 49 AEs are classified into three clusters: 1) AEs associated with signs and symptoms of muscle injury, 2) AEs associated with laboratory tests for muscle injury, and 3) AEs associated with kidney injury and its laboratory diagnosis and treatment.

data("statin49")
head(statin49)
#>                    Atorvastatin Fluvastatin Lovastatin Pravastatin Rosuvastatin
#> Rhabdomyolysis             2041          52         44         163          936
#> Muscle Disorder             291           2          7          21          191
#> Muscle Fatigue               85           0          2          16           30
#> Muscle Haemorrhage           24           0          0           5           13
#> Muscle Necrosis              68           2          0           1           10
#> Muscle Rupture              181          25          0          61           36
#>                    Simvastatin Other
#> Rhabdomyolysis            1376 31707
#> Muscle Disorder             87  7329
#> Muscle Fatigue              39  4257
#> Muscle Haemorrhage           4  3806
#> Muscle Necrosis             20   662
#> Muscle Rupture             120  3219

data("statin49_AE_idx")
head(statin49_AE_idx)
#>   idx                 AE
#> 1   1     Rhabdomyolysis
#> 2   1    Muscle Disorder
#> 3   1     Muscle Fatigue
#> 4   1 Muscle Haemorrhage
#> 5   1    Muscle Necrosis
#> 6   1     Muscle Rupture

Adverse Event (AE) Identification with MDDC

Using Boxplot Method

Our goal is to identify (AE, drug) pairs with abnormally high report counts, specifically those cells with counts significantly exceeding their expected values.

First we perform the analysis using mddc_boxplot(). This function has five argument:

contin_table: A data matrix of an $I \times J$ contingency table with rows representing adverse events and columns representing drugs. We recommend users first check the input contingency table using the function check_and_fix_contin_table().
col_specific_cutoff: Logical. In step 2 of the algorithm, whether to apply the boxplot method to the standardized Pearson residuals within each drug column (default is TRUE) or to the entire table (FALSE).
separate: Logical. In step 2 of the algorithm, whether to separate the standardized Pearson residuals for the zero cells and non zero cells and apply boxplot method separately or together. Default is TRUE.
if_col_cor: Logical. In step 3 of the algorithm, whether to use column (drug) correlation or row (adverse event) correlation. Default is FALSE, indicating the use of adverse event correlation. TRUE indicates the use of drug correlation.
cor_lim: A numeric value between 0 and 1. Specifies the correlation threshold to select “connected” adverse events in step 3. Default is 0.8.
coef: A numeric value or a list of numeric values. If a single numeric value is provided, it will be applied uniformly across all columns of the contingency table. If a list is provided, its length must match the number of columns in the contingency table, and each value will be used as the coefficient for the corresponding column.
num_cores: Number of cores used to parallelize the MDDC Boxplot algorithm. Default is 2.

We now perform the MDDC (boxplot) analysis with the statin49 dataset:

set.seed(42)
test1 <- mddc_boxplot(
  contin_table = statin49,
  col_specific_cutoff = T,
  separate = T,
  if_col_cor = F,
  cor_lim = 0.8,
  coef = 1.5
)

The above function outputs a list with three components:

boxplot_signal: An $I\times J$ data matrix with entries 1 or 0, indicating the signals identified in step 2. A value of 1 indicates signals, 0 indicates no signal.
corr_signal_pval: An $I\times J$ data matrix of p-values for each cell in the contingency table from step 5, when the $r_{ij}$ values are mapped back to the standard normal distribution.
corr_signal_adj_pval: An $I\times J$ data matrix of the Benjamini-Hochberg adjusted p-values for each cell in step 5. Users can choose whether to use corr_signal_pval or corr_signal_adj_pval, and can set their own p-value threshold (for example, 0.05).

Below, we display the first few rows and columns for each component of test1. We first check the component boxplot_signal:

head(test1$boxplot_signal)[, 1:5]
#>                    Atorvastatin Fluvastatin Lovastatin Pravastatin Rosuvastatin
#> Rhabdomyolysis                1           0          0           1            1
#> Muscle Disorder               0           0          0           0            1
#> Muscle Fatigue                0           0          0           0            0
#> Muscle Haemorrhage            0           0          0           0            0
#> Muscle Necrosis               0           0          0           0            0
#> Muscle Rupture                0           0          0           1            0

This indicates the pairs (Rhabdomyolysis, Atorvastatin), (Rhabdomyolysis, Pravastatin), (Muscle Rupture, Pravastatin), (Rhabdomyolysis, Rosuvastatin), and (Muscle Disorder, Rosuvastatin) are identified as signals in step 2 of MDDC (boxplot). Now we look at the second component corr_signal_pval which shows the p-values of all the cells from step 5:

round(head(test1$corr_signal_pval)[, 1:5], digits = 3)
#>                    Atorvastatin Fluvastatin Lovastatin Pravastatin Rosuvastatin
#> Rhabdomyolysis               NA          NA         NA          NA           NA
#> Muscle Disorder           0.527       0.974      0.178       0.545        0.000
#> Muscle Fatigue            0.556       0.834      0.252       0.061        0.656
#> Muscle Haemorrhage        0.561       0.635      0.521       0.307        0.570
#> Muscle Necrosis           0.534       0.186      0.869       0.835        0.677
#> Muscle Rupture            0.569       0.019      0.999       0.000        0.678

In this output, we observe that the first row, corresponding to the adverse event “Rhabdomyolysis”, does not have associated p-values. This is because, in step 2 of the algorithm, “Rhabdomyolysis” was already identified as an AE signal for Atorvastatin, Pravastatin, Rosuvastatin, and Simvastatin. Consequently, the standardized Pearson residual values for these four drugs were replaced with NA. With only two residual values remaining in the first row, it was not possible to find connected AEs for “Rhabdomyolysis”. Therefore, this adverse event was excluded from the subsequent steps of the analysis. Note that for computing the Pearson correlation in step 3, at least three values are required in the matching positions. Applying a p-value threshold of 0.05, we identify the following pairs as signals by considering AE correlations: (Muscle Rupture, Fluvastatin), (Muscle Rupture, Pravastatin), and (Muscle Disorder, Rosuvastatin).

The third component, corr_signal_adj_pval, provides the Benjamini-Hochberg adjusted p-values. Users can choose whether to use corr_signal_pval or corr_signal_adj_pval and can set their own p-value threshold (for example, 0.05).

Function for Finding Optimal Boxplot Coefficient

We provide a function that outputs appropriate coefficients for boxplot using a grid search method to control the FDR. This function takes the following arguments:

contin_table: A matrix representing the $I \times J$ contingency table.
n_sim: An integer specifying the number of simulated tables under the assumption of independence between rows and columns. Default is 1000.
target_fdr: A numeric value specifying the desired level of false discovery rate (FDR). Default is 0.05.
grid: A numeric value representing the size of the grid added to the default value of coef = 1.5 as suggested by Tukey. Default is 0.1.
col_specific_cutoff: Logical. If TRUE, then a single value of the coefficient is returned for the entire dataset, else when FALSE specific values corresponding to each of the columns are returned.
exclude_small_count: A logical indicating whether to exclude cells with counts smaller than or equal to five when computing boxplot statistics. Default is TRUE.

We apply this function to the statin49 dataset:

set.seed(42)
find_optimal_coef(
  contin_table = statin49,
  n_sim = 1000,
  target_fdr = 0.05,
  grid = 0.1,
  col_specific_cutoff = TRUE,
  exclude_small_count = TRUE
)
#> $coef
#> [1] 2.5 3.2 2.8 2.7 2.6 2.4 2.0
#> 
#> $FDR
#> [1] 0.050 0.044 0.050 0.049 0.047 0.038 0.044

This function outputs a list with the following components:

coef: A numeric vector containing the optimal coefficient ‘coef’ for each column of the input contingency table.
FDR: A numeric vector with the corresponding false discovery rate (FDR) for each column.

Using the Monte Carlo Method

Next, we introduce another primary function of this package, mddc_mc(), which implements the MDDC (MC) algorithm. This function has the following arguments:

contin_table: A data matrix of an $I\times J$ contingency table with rows representing adverse events and columns representing drugs. We recommend users first check the input contingency table using the function check_and_fix_contin_table().
quantile_mc: In step 2 of the algorithm, this specifies the quantile of the null distribution obtained via the Monte Carlo (MC) method to use as a threshold for identifying cells with high values of standardized Pearson residuals. The default is 0.95.
mc_num: The number of Monte Carlo replications to perform in step 2. The default is 10,000.
exclude_same_drug_class: In step 2, when applying Fisher’s exact test to cells with a count less than six, a $2\times2$ contingency table is constructed. This argument specifies whether to exclude other drugs in the same class as the drug of interest. The default is TRUE.
col_specific_cutoff: Logical. Specifies whether to apply the MC method to the standardized Pearson residuals of the entire table or within each drug column in step 2. The default is TRUE, indicating column-specific cutoff. FALSE applies the MC method to the residuals of the entire table.
separate: Logical. In step 2 of the algorithm, indicates whether to separate the standardized Pearson residuals for zero cells and non-zero cells, applying the MC method separately. The default is TRUE.
if_col_cor: Logical. In step 3 of the algorithm, specifies whether to use column (drug) correlation or row (adverse event) correlation. The default is FALSE, indicating the use of adverse event correlation. TRUE indicates the use of drug correlation.
cor_lim: A numeric value between 0 and 1. Specifies the correlation threshold to use in step 3 for selecting “connected” adverse events. The default is 0.8.
num_cores: Number of cores used to parallelize the MDDC Boxplot algorithm. Default is 2.
seed: An optional integer to set the seed for reproducibility. If NULL, no seed is set.

We now apply MDDC (MC) algorithm to statin49 using the following code:

set.seed(42)
test2 <- mddc_mc(
  contin_table = statin49,
  quantile = 0.95,
  rep = 10000,
  exclude_same_drug_class = T,
  col_specific_cutoff = T,
  separate = T,
  if_col_cor = F,
  cor_lim = 0.8
)

This function outputs a list with five components:

mc_pval: Returns the p-values for each cell in step 2. For cells with counts greater than five, the p-values are obtained via the Monte Carlo (MC) method. For cells with counts less than or equal to five, the p-values are obtained via Fisher’s exact tests.
mc_signal: Indicates signals for cells with counts greater than five, identified in step 2 by the MC method. A value of 1 indicates a signal, while 0 indicates no signal.
fisher_signal: Indicates signals for cells with counts less than or equal to five, identified in step 2 by Fisher’s exact tests. A value of 1 indicates a signal, while 0 indicates no signal.
corr_signal_pval: Returns the p-values for each cell in the contingency table in step 5, where the $r_{ij}$ values are mapped back to the standard normal distribution.
corr_signal_adj_pval: Returns the Benjamini-Hochberg adjusted p-values for each cell in step 5. Users can choose whether to use corr_signal_pval or corr_signal_adj_pval, and select an appropriate p-value threshold (for example, 0.05).

Function for Reporting

This package includes a postprocessing function report_drug_AE_pairs() for display the identified (AE, drug) pairs as well as the observed count, expected count and the standardized Pearson residuals for the pairs. This function takes two arguments:

contin_table: A data matrix representing an $I \times J$ contingency table, with rows corresponding to adverse events and columns corresponding to drugs.
contin_table_signal: A data matrix with the same dimensions and row and column names as contin_table. Entries should be either 1 (indicating a signal) or 0 (indicating no signal). This matrix can be obtained by applying the mddc_boxplot() or mddc_mc() functions to contin_table.

Now we apply this function to the second component mc_signal we obtained above and display the first few rows:

test3 <- report_drug_AE_pairs(
  contin_table = statin49,
  contin_table_signal = test2$mc_signal
)

head(test3)
#>           drug                 AE observed_num expected_num std_pearson_res
#> 1 Atorvastatin     Rhabdomyolysis         2041     112.0567        182.5555
#> 2 Atorvastatin    Muscle Disorder          291      24.4606         53.9791
#> 3 Atorvastatin     Muscle Fatigue           85       13.665         19.3279
#> 4 Atorvastatin Muscle Haemorrhage           24      11.8848          3.5198
#> 5 Atorvastatin    Muscle Necrosis           68       2.3541         42.8516
#> 6 Atorvastatin     Muscle Rupture          181      11.2368          50.723

These (AE, drug) pairs are part of the signals identified by the MDDC (MC) method in step 2 for pairs with counts greater than five. Similarly, we can apply this function to the signals obtained from the correlation steps using the following code. Here we use a threshold of 0.05 for selecting the signals from step 5. We omit the output for brevity.

report_drug_AE_pairs(
  contin_table = statin49,
  contin_table_signal = test2$corr_signal_pval < 0.05
)
#>            drug                                        AE observed_num
#> 1  Atorvastatin                 Diaphragm Muscle Weakness           14
#> 2  Atorvastatin     Blood Creatine Phosphokinase Abnormal           34
#> 3  Atorvastatin                            Myoglobinaemia           15
#> 4   Fluvastatin                             Myoglobinuria            4
#> 5   Fluvastatin                          Renal Impairment           52
#> 6    Lovastatin                       Myasthenic Syndrome            9
#> 7  Rosuvastatin Blood Creatine Phosphokinase Mm Increased            9
#> 8  Rosuvastatin                   Blood Calcium Decreased          110
#> 9  Rosuvastatin      Creatinine Renal Clearance Decreased          124
#> 10  Simvastatin                            Myopathy Toxic           21
#> 11  Simvastatin     Blood Creatine Phosphokinase Abnormal           11
#> 12        Other                             Renal Failure       250710
#>    expected_num std_pearson_res
#> 1         0.361         22.7358
#> 2        0.9688         33.6109
#> 3        0.2376         30.3341
#> 4        0.0302          22.827
#> 5        9.3488         13.9613
#> 6        0.0334         49.0479
#> 7        0.0478         40.9642
#> 8       30.7404         14.3109
#> 9       15.1319         28.0154
#> 10       0.6838         24.5848
#> 11       0.4194         16.3495
#> 12  250051.2658         15.9753

Simulating datasets with grouped AEs

This package offers a data generation function for simulating pharmacovigilance datasets, with the option to incorporate grouped AEs. This function can embed correlations between the standardized Pearson residuals for AEs and takes the following arguments:

row_marginal: Marginal sums for the rows of the contingency table.
column_marginal: Marginal sums for the columns of the contingency table.
signal_mat: A data matrix of the same dimensions as the contingency table with entries indicating the signal strength. Values must be greater than or equal to 1, where 1 indicates no signal, and values greater than 1 indicate a signal.
contin_table: A data matrix representing an $I \times J$ contingency table with rows corresponding to adverse events and columns corresponding to drugs. The row and column marginals are used to generate the simulated data.
AE_idx: A data frame with two variables, idx and AE, where idx indicates the cluster index (either a name or a number), and AE lists the adverse event names. An example named AE_idx, which provides the AE group index for the statin49 dataset, is included in the package.
n_rep: The number of simulated contingency tables to be generated.
rho: A numeric value representing the correlation of the AEs within each cluster. The default is 0.5.
seed: An optional integer to set the seed for reproducibility. If NULL, no seed is set.

Now we demonstrate the usage of this function by generating three simulated datasets based on the marginals of statin49. First, we need to create a data matrix with the same dimensions as statin49 that indicates the signal strength for each (AE, drug) pair. In this example, we assign a signal (Rhabdomyolysis, Atorvastatin) with a strength of 4 to the simulated dataset:

# create a matrix indicating signal strength
sig_mat <- matrix(1,
  nrow = nrow(statin49),
  ncol = ncol(statin49)
)

# assign (Rhabdomyolysis, Atorvastain) as a signal
# with a signal strength 4
sig_mat[1, 1] <- 4

The 49 AEs in statin49 can be grouped into three clusters, as listed in the statin49_AE_idx: 1) AEs associated with signs and symptoms of muscle injury, 2) AEs associated with laboratory tests for muscle injury, 3) AEs associated with kidney injury and its laboratory diagnosis and treatment. Next we take a look at the first few rows of sttain49_AE_idx, which indicate the group index of each AE in statin49:

head(statin49_AE_idx)
#>   idx                 AE
#> 1   1     Rhabdomyolysis
#> 2   1    Muscle Disorder
#> 3   1     Muscle Fatigue
#> 4   1 Muscle Haemorrhage
#> 5   1    Muscle Necrosis
#> 6   1     Muscle Rupture

Now we generate 3 simulated contingency tables based on the marginals of statin49, the pre-specified matrix of signal strength, and the AE group index, with a within group correlation $\rho=0.5$ :

sim_dat <- generate_contin_table_with_clustered_AE(
  contin_table = statin49,
  n_rep = 3,
  AE_idx = statin49_AE_idx,
  rho = 0.5,
  signal_mat = sig_mat,
  seed = 42
)

This function returns a list of simulated contingency tables, with the length of the list equal to the number of replications specified in the argument n_rep. In this example, we have n_rep = 3. Now we perform the MDDC (MC) analysis on the first simulated contingency table and extract the identified pairs from step 2:

test5 <- mddc_mc(sim_dat[[1]], seed = 42)
report_drug_AE_pairs(
  contin_table = sim_dat[[1]],
  contin_table_signal = test5$mc_signal
)
#>           drug             AE observed_num  expected_num std_pearson_res
#> 1 Atorvastatin Rhabdomyolysis          455      113.3504         32.1489
#> 2        Other       Other AE     61678474 61677840.4692          5.6996

In the output, there is the pair (Rhabdomyolysis, Atorvastatin) identified, which matches what we embedded.

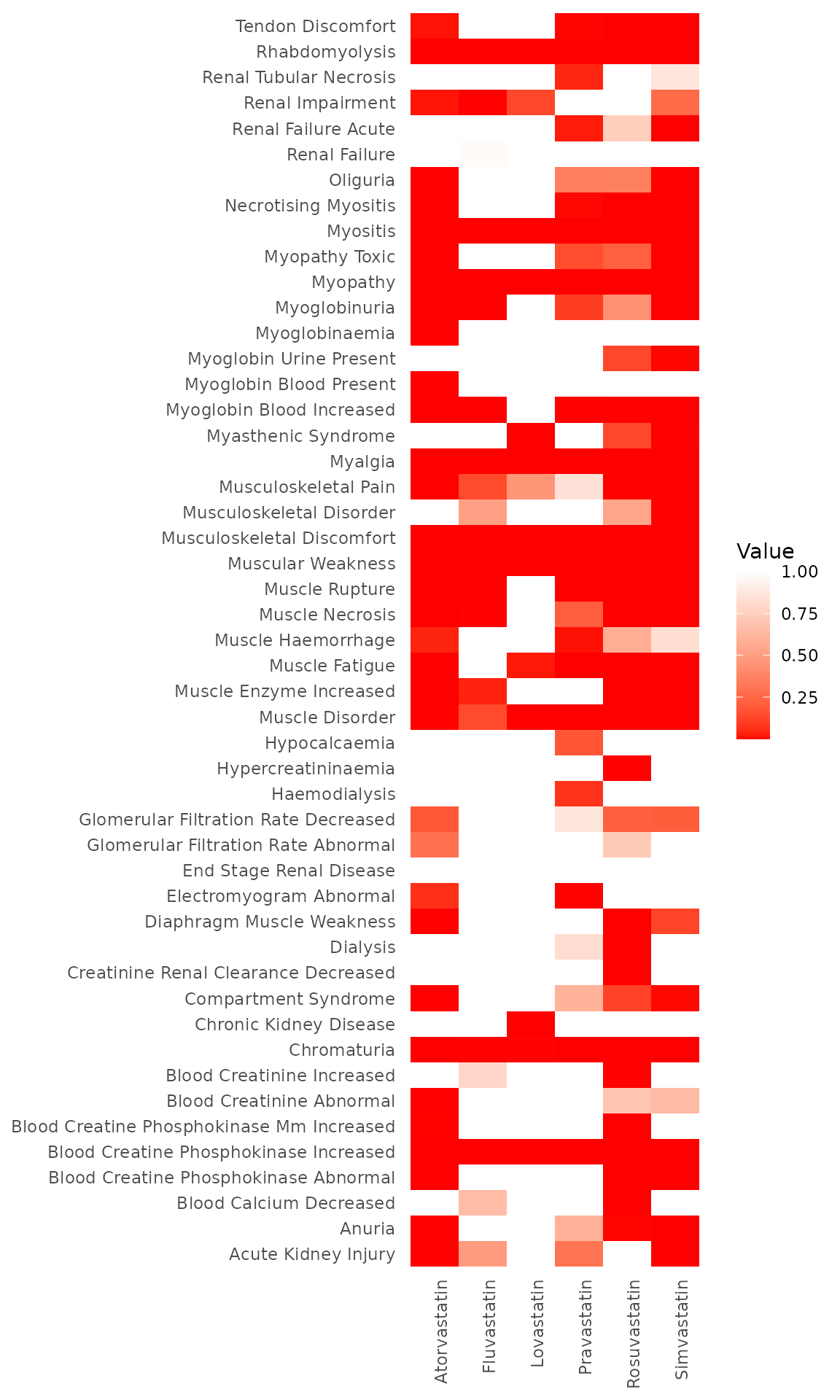
Visualization

We have also included heatmap visualizations as a part of our package to help visualize the identified signals or p-values.

This function takes the following arguments:

data: A matrix or data frame to be visualized as a heatmap. The row names and column names of the data will be used for labeling the heatmap axes.
cell_width: Numeric value indicating the width of each cell in the heatmap. Default is 1.
cell_height: Numeric value indicating the height of each cell in the heatmap. Default is 1.

The following heatmap shows the visualization of the associated p-values of Monte Carlo method in step 2:

plot_heatmap(test2$mc_pval[-50, -7])